TREES, your friendly neighbourhood data structures.


What is a Tree?

A Tree is a non-linear data structure that organizes data in a hierarchical way.
As opposed to arrays or linked lists that are linear, a tree can have zero or more child nodes.

Structure of a tree.

The tree data structure is a collection of nodes. These nodes are connected to each other by edges. Each node contains a value (data) and may or may not have a child node.

A tree usually starts with a single root/parent node. Every child of the tree descends from this particular root node. Moreover, every child node descends from only one parent node. Also, the parent child relationships are unidirectional.
The nodes at the very end of each branch are called as the leaf nodes .

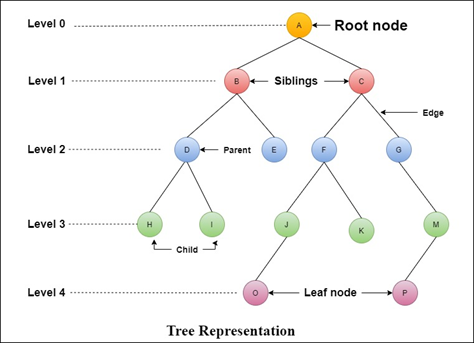
tree data structure
In the tree above:
  A is a parent of B and C.
  B is called a child of A.
  B and C are siblings to each other.
  E, H, I, K, O and P are leaves.
  Also, D is a parent for nodes H and I.

Some real world use cases:
  1. Facebook comments show this behaviour when you comment on a post. And then, someone else comments on your comment.
  2. Web pages are created by something called as the DOM. And this, is nothing but a tree data structure.
  3. Abstract Syntax Trees or ASTs are tree representations of code. They are a fundamental part of the way a compiler works.
  4. Linked list is a technically a type of tree, but with just one single path i.e; they are linear.
What is a Binary Tree?

A binary tree is a tree data structure composed of nodes, each of which has at most, two children, referred to as left and right nodes. The tree starts off with a single node known as the root.

For a binary tree, each node has a value associated with it and two other pointers.
  1. One to the left of the node, called as the left child .
  2. The other to the right of the node, called as the right child .
In order for a tree to qualify as a binary tree, each and every node should satisfy the following criterias:

  1. Each node can have either zero, one or two child nodes only.
  2. Each child node can have only one parent.
  3. Each node represents a certain state.

Height and depth of a binary tree.

The height of a node is the number of edges on the longest path from the node to a leaf.  A leaf node will have a height of zero.

The depth of a node is the number of edges frpm the node to the tree's root node.  A root node will have a depth of zero.

Types of Binary Trees:
  1. Full Binary Tree. : All the nodes have zero or two children, except for the leaf nodes.
  2. Complete Binary Tree.: All levels are completely filled, except for the lowest one, which is filled from the left.
  3. Perfect Binary Tree. : Completely filled out i.e; a node either has zero or two children. Also, the bottom layer is completely filled.
What is a binary search tree?

A binary search tree (BST) is a binary tree where each node has a comparable key (and an associated value) and satisfies the restriction that the key in any node is larger than the keys in all nodes in that node's left subtree and smaller than the keys in all nodes in that node's right subtree.

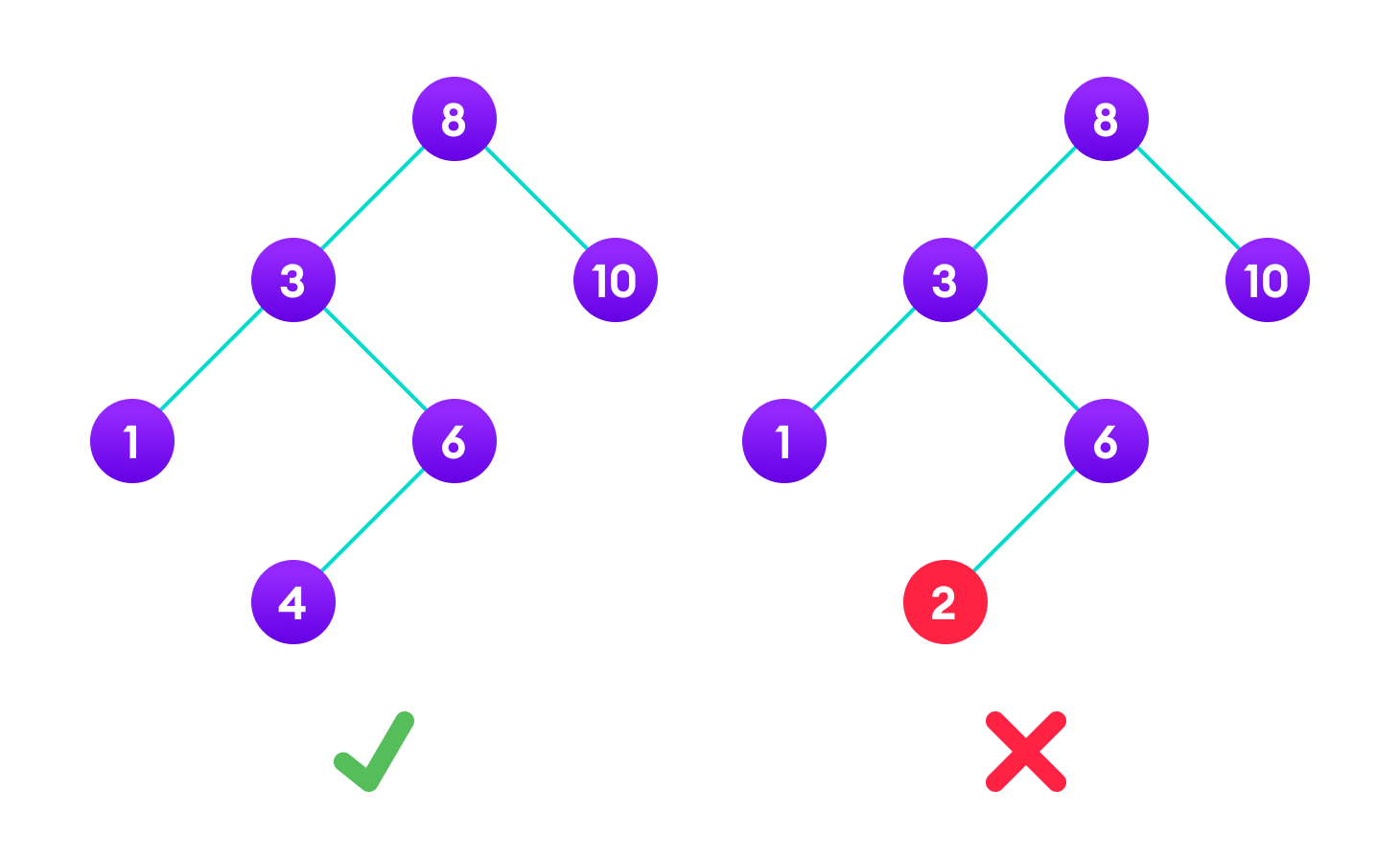
facebook comments are made up of tree data structure

Among the trees represented above, the one on the left hand side follows the criteria that all the nodes in the left hand side of a particular node have key value less than that of the parent node and all on the right are greater than that of the parent. Hence, it is safe to say that it is a BST.
However, for the one on the right hand side all but the last node; i.e node with a value of two lies on the right hand side of it's grand parent(node with a value of three), which stops it from being qualified as a BST.

Advantages of using a binary search tree.
  1. Searching become very efficient in a binary search tree since, we get a hint at each step, about which sub-tree contains the desired element.
  2. The binary search tree is considered as efficient data structure in comparison to arrays and linked lists. In searching process, it removes half sub-tree at every step. Searching for an element in a binary search tree takes O(log2n)   time. In worst case, the time it takes to search an element is O(n)  .
  3. It also speeds up the insertion and deletion operations as compared to that in array and linked list.
Implementing a BST.
For the implementation, we'll use an auxiliary Node class that will store int values, and keep a reference to each child:
class Node {
       int data ;
       Node left ;
       Node right ;
          Node(int data) {
             this.data = data ;
             right = null ;
             left = null ;
          }
     }

Common operations on a BST :
  1. Search for a node
    2. boolean searchRec(Node root, int data) {
           if(root == null)
             return false ;
              if(root.data > data )
                   return searchRec(root.left , data) ;
              else if(root.data < data )
                   searchRec(root.right , data) ;
              else if(root.data == data )
                   return true ;
         }

  2. Insert a new node
    3. In order to insert a new node, first find the place where you should insert the node( so as to satisy the BST condition).
    Node insertRec(Node root, int data) {
           if(root == null) {
             root=new Node(data);
             return root;
           }
              if(root.data > data )
                 root.left = insert(root.left , data);
              else if(root.data < data )
                 root.right = insert(root.right , data);
           return root;
         }

  3. Delete a node
    4. In order to delete a node, first search for the node that you want to delete. Once that is done, there can be three cases that can arise.
    • Case 1 : If the node to be deleted has no child, make it null.
    • Case 2 : If the node to be deleted has one child, copy the child at node's positon.
    • Case 3 : If the node to be deleted has two children, replace the node with inorder successor.

    Let's dive into the code now.
    Node deleteRec(Node root, int data) {
      if(root == null) {
           return root ;
         }
           if(root.data > data )
              root.left = deleteRec(root.left , data) ;
           else if(root.data < data )
              root.right = deleteRec(root.right , data) ;
           else {
              if(root.left == null )
                 return root.right ;
              if(root.right == null )
                 return root.left ;
             root.data = inOrderSuccessor(root.right);
             root.right = deleteRec(root.right , root.data);
              }
         return root;
      }

If you would like to know more about BST's, their drawbacks, how to improve their performance by using AVL trees?
Click here.

Conclusion

That’s a lot of vocabulary for one tiny tree! Trees don’t stay tiny for long! Keep working at understanding trees by learning how to implement them, about their time and space complexity, and where they work best!

Thanks for reading this.🙏🏻


   Set your mood?